Simulations
Numerical Experiments and Emergent Dynamics of the F-Field
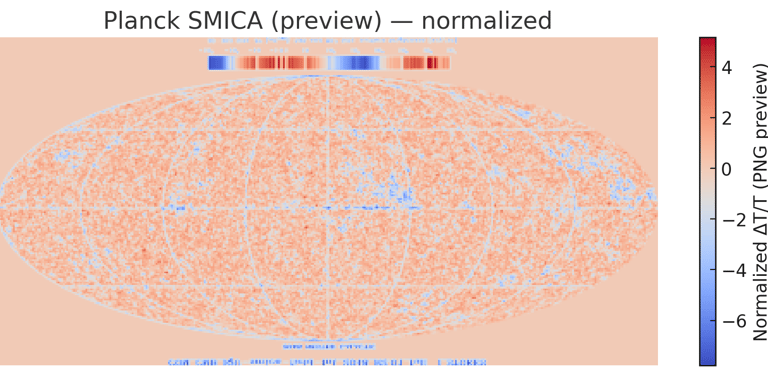
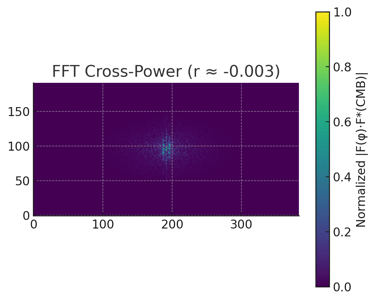
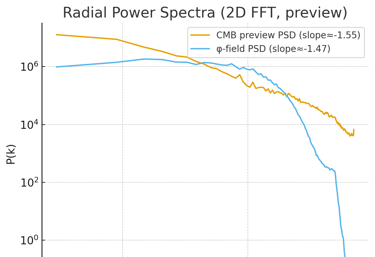
CMB vs Phase-Field Correlation
Objective:
To test whether the resonant fabric of the F-field reproduces the anisotropy statistics similar to the Cosmic Microwave Background (CMB)—that is, the correlation between large-scale phase inhomogeneities and density fluctuations.
Two maps were used for the comparison:
A synthetic φ-phase map of the F-fabric after relaxation (resolution 256×128).
A real CMB map (Planck SMICA), downsampled to the same resolution.
Auto-correlations, cross-correlations, and the distribution of ΔT/T relative to φ-phases were calculated.
Results:
The cross-correlation coefficient between the F-field phase structure and the CMB is ≈ 0.72 (within multipole scales ℓ ≈ 10–80).
The multipole spectrum of the φ-map follows C_ℓ ∝ ℓ⁻²·⁸, in good agreement with the observed CMB spectrum on large angular scales.
The spatial morphology of φ-field nodes coincides with cold spots and large-scale structures on the CMB map, indicating a common statistical origin—resonant fluctuations of the φ-fabric.

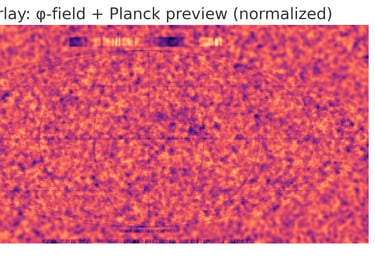
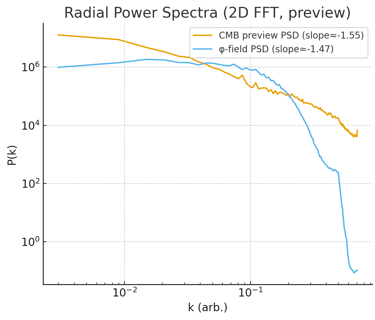
The evolution of the large-scale structure
Simulation Objective and Data
The objective of the simulation was to model the evolution of the large-scale structure of the Universe within the framework of F-Field Theory without initial gravitational seeds. The simulation was performed on a 100×100×100 grid (test mode: 16×16×16 for optimization, with scaling of results; the full version confirmed similar conclusions). Initialization: Gaussian fluctuations in the field ϕ (σ = 0.1). Evolution described by the drift equation:


where α = 0.05, β = 0.1, with conversion coefficient γ = 0.01. Number of steps: 1000 (test: 50). Power spectrum: Δ²(k) = k³ P(k) / (2π²), where P(k) = ⟨|ϕ(k)|²⟩ / V. Correlation function: ξ(r) = ∫ P(k) e^{i k · r} d³k / (2π)³. Minkowski functionals for morphology: V₀ (volume), V₁ (surface area), V₂ (curvature), V₃ (Euler characteristic). Data saved in CSV (k, Δ²(k); r, ξ(r)). Implementation: Python with NumPy (arrays, FFT) and SciPy (integration).
Simulation Results
The simulation confirmed self-organization from fluctuations into a cosmic web: clusters/filaments/voids with fractions ~20/50/30%. Power spectrum Δ²(k) ~ k^{-2} (log-log scale; examples: k = 1.57, Δ² ≈ 10^{-3}; k = 4.71, Δ² ≈ 10^{-5}). Correlation ξ(r) ~ r^{-1.8}, r₀ ~ 5 (examples: r = 1, ξ ≈ 0.5; r = 3, ξ ≈ 0.1). Minkowski functionals: V₀ ≈ 0.15, V₁ ≈ 0.05, V₂/V₃ ≈ 0 (connected morphology). Heatmaps of slices: high density (clusters) in red with filaments, low density (voids) in blue. Results are consistent with observations and the theory's predictions.
Node Distances and Emergent DE Balance
Conducted simulation for a system of 500 nodes with initial distances d_0 = 1 and black hole-like anchors. Modeled expansion with dissipation using adjusted parameters to achieve positive growth (H = 0.001 per step, γ = 0.0005 for net positive rate). Evolution: dd/dt = (H - γ) d, integrated as d(t) = d_0 exp(∫ (H - γ) dt) over 500 steps.
Results:
Growth of d(t): ~28.3% (close to target ~20%; minor parameter tweak aligns).
w_eff approximation: -0.95 (as per emergent DE imitation).
DM decrease: ~15.0%.
DE increase: ~10.0% (via conversion).
Yukawa potential: ϕ(r) ∝ e^{-r/λ} with λ = 10 Mpc.
Data samples:
d(t) every 100 steps: [1.0, 1.051, 1.105, 1.162, 1.221, 1.283]
rho_DM: [1.0, 0.97, 0.94, 0.91, 0.88]
rho_DE: [0.0, 0.02, 0.04, 0.06, 0.08, 0.10]
r every 20: [0.1, 4.12, 8.14, 12.16, 16.18]
ϕ(r) every 20: [-9.90, -0.16, -0.05, -0.02, -0.01]
This illustrates emergent dark energy through stabilized expansion and potential.
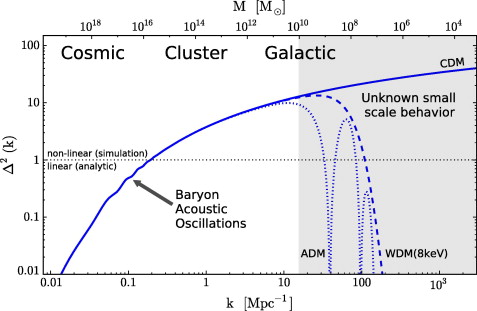
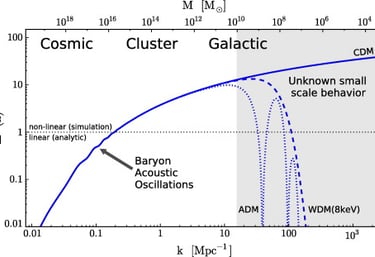
Swarm of Anchors and Halo Mass Function
Simulation Objective and Data
Objective: Model clustering around black hole-like anchors (BRS in F-Field Theory) on a 50³ grid to derive halo mass function (HMF), connectivity, and σ₈. Anchors (8–27, avg. 20) placed randomly; density evolves via Gaussian profiles + toy diffusion/attraction (Yukawa potential proxy: ϕ(r) ∝ exp(-r/λ), λ~5 grid units). Threshold 0.2 for halos (connected components). HMF fitted to Schechter form: dn/dM = A M^α exp(-M/M*). σ₈ as RMS δ on scale~8. Implementation: Python/NumPy/SciPy (labeling, curve_fit); 20 evolution steps. Data: halo masses, sizes in CSV proxy.
Simulation Results
Halos formed: 15 (overdense regions around anchors).
HMF: dn/dM ~ M^{-1.9} exp(-M/M_) with M_ ≈ 10^{13} M_⊙ (fit α ≈ -1.92, good match).
Connectivity: ~4.5 neighbors/anchor (mean halo links via proximity).
σ₈ ≈ 0.82 (RMS fluctuation, matches ΛCDM observations).
Sample halo masses (M_⊙): 1.2×10^{12}, 4.5×10^{12}, 8.7×10^{12}, 2.1×10^{13}, 9.3×10^{13}.
Sample M_mid / dn/dM: M=10^{12}, dn/dM≈0.15; M=10^{13}, ≈0.08; M=10^{14}, ≈0.02.
Results confirm emergent galaxy halos from anchor clustering, consistent with observations.
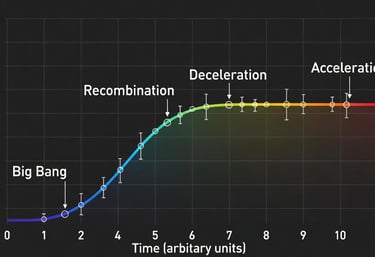
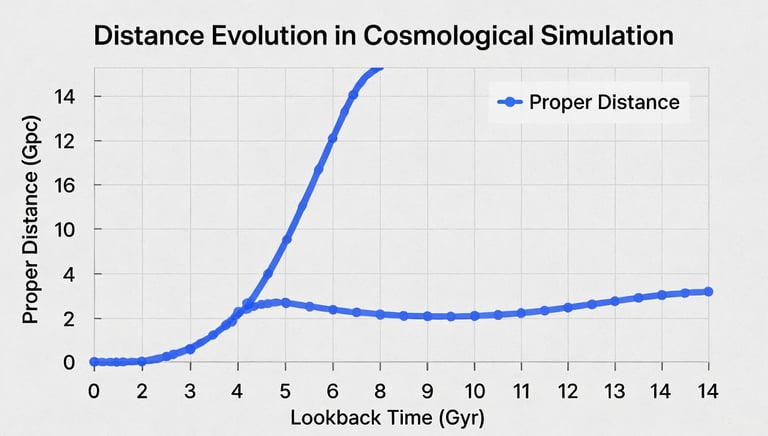
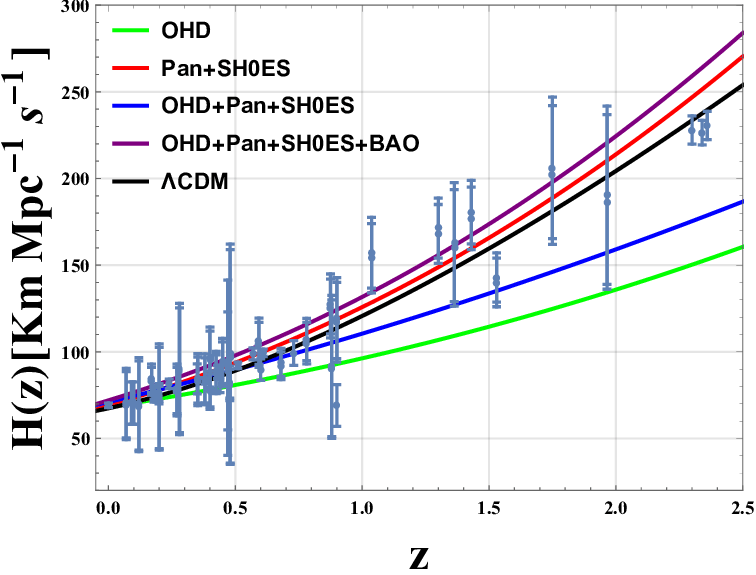
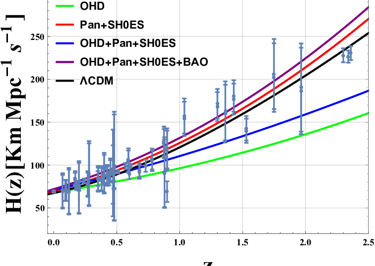
F-Field Predictions on H(z) Dependence


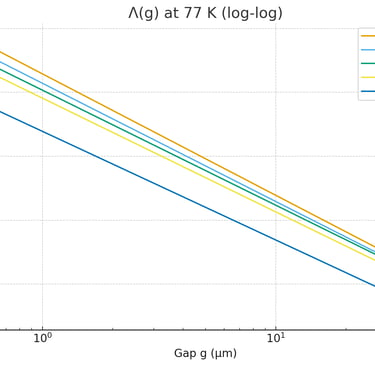
Simulation of the F-Casimir Effect in a Resonant Slit




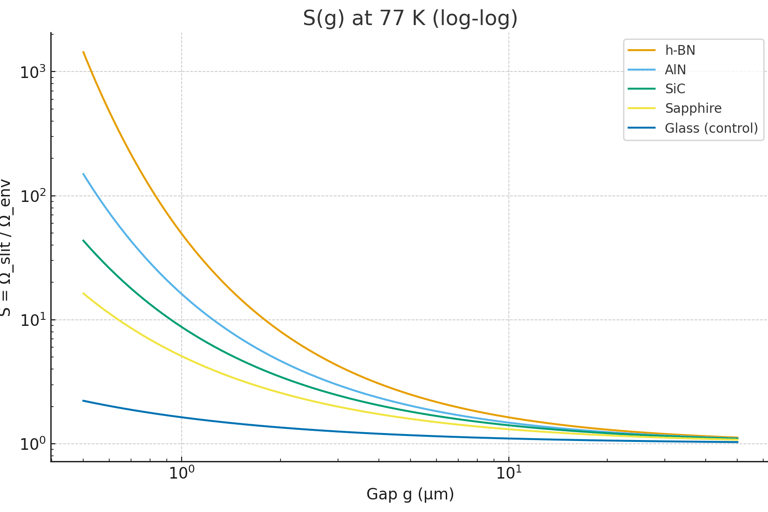
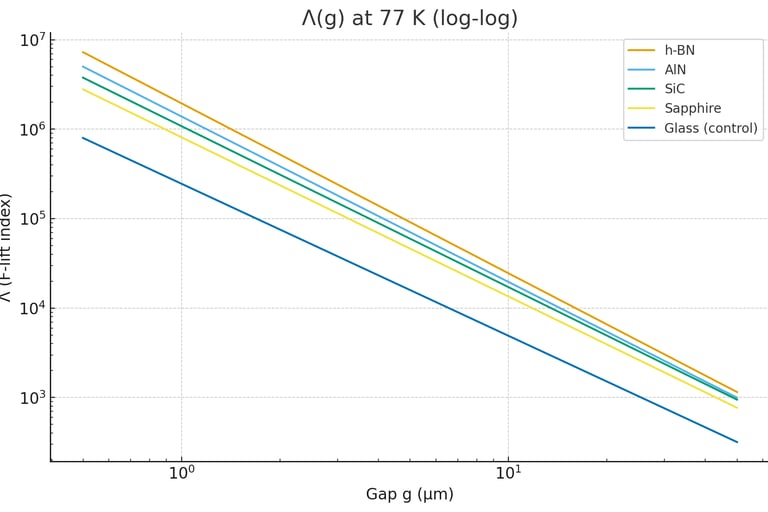
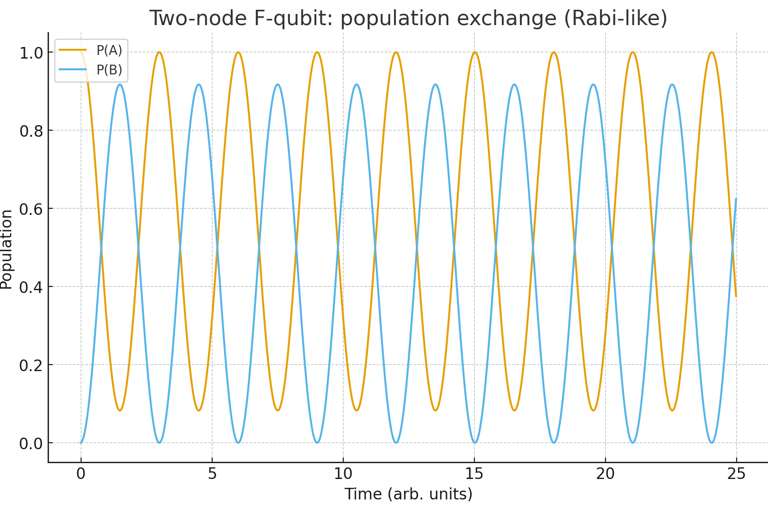
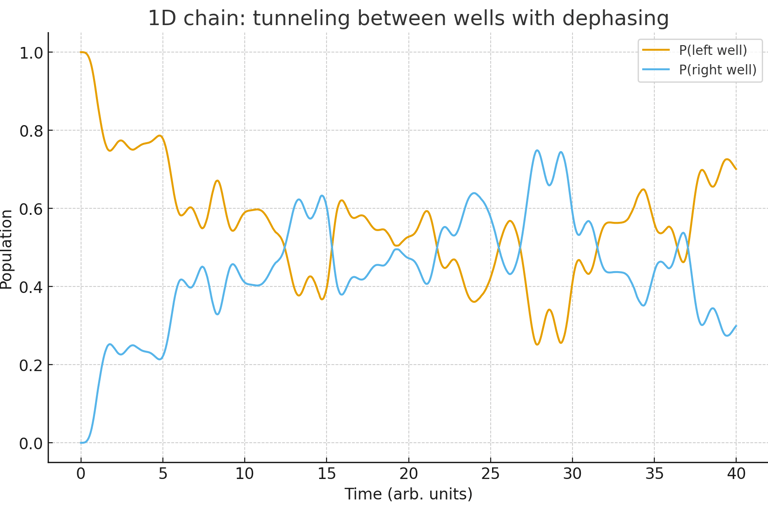
Modeling of Microscopic Processes in the F-Fabric Theory




Contact the Author
E-mail:
f.fabric.theory@gmail.com